Wissen ist ein Privileg. Die Weitergabe eine Pflicht.

Dirk Freyling unabhängiger Forscher & Künstler

[Technischer Hinweis: Sollten Sie ungewollt diese Webseite als Solo-Webseite ohne Webseitenmenü ("frame-los") vorliegen haben, so gelangen Sie hier zur kompletten menügesteuerten Elementarkörpertheorie-Webseite....

           

 

Das Newtonsche Gravitationsgesetz erlebt im Rahmen der Elementarkörpertheorie eine unerwartete Renaissance. Das Hinterfragen des scheinbar Banalen führt zu neuen Ideen und eröffnet Transparenz und Gesamtheit, die begeistern. Das Geheimnis der "scheinbar" sehr schwachen Gravitation im Verhältnis zur elektrischen Wechselwirkung und starken Wechselwirkung liegt in der falschen Annahme begründet, daß es generell einen Masse entkoppelten Raum gibt. Berücksichtigt man den Raum, den makroskopische Körper sowohl durch ihre Objektausdehnung als auch durch ihren Wechselwirkungsradius aufspannen, dann wird deutlich, daß die "fehlende" Energie in dem Raum selbst "steckt". Im Rahmen der Elementarkörpertheorie lässt sich u.a. (die) «Raumenergie» plausibel verstehen und berechnen.

Die Divergenzproblematiken, sowohl klassischer als auch quantenfeldtheoretischer Betrachtungen, finden ihre theoriebeladene Ursache in den jeweiligen Denkmodellen. Dort wird die innere Struktur der Energieträger (Gravitation, (elektrische) Ladung) schlicht nicht erfasst. Berücksichtigt man jedoch die endliche, realphysikalisch orientierte, phänomenologische Natur der Objekte, lösen sich die "Unendlichkeiten" plausibel auf.

Übrigens: Die Erde bewegt sich nicht um die Sonne. Wie schon Isaac Newton in seinen Principa 1687 festgestellt hat, bewegen sich Sonne und Planeten um den Massenschwerpunkt des Sonnensystems, genannt Baryzentrum.

 

Vorwort

Schon Isaac Newton hielt die Vorstellung, daß Gravitation durch den leeren Raum wirken könne, (berechtigterweise) für absurd. Es ist - übergeordnet und insgesamt betrachtet - alles andere als trivial, Raum und Zeit als physikalische "Gegenstände" zu betrachten. Raum und Zeit sind primär "Ordnungsmuster des Verstandes". Um aus diesen Ordnungsmustern Physik zu "erhalten", bedarf es zwingend einer phänomenologischen Betrachtung und Erklärung.

"abstract"

 

Die im "bekannten" Newtonschen Gravitationsgesetz verwendete Gravitationskonstante γG bezieht sich auf den "längen-kleinsten" Körper G {Elementarquant}. Dieser Sachverhalt ist nicht offensichtlich, da das "üblich formulierte" Gravitationsgesetz diesen ursprünglichen Zusammenhang nicht explizit offenbart.

Das Geheimnis der "scheinbar" sehr schwachen Gravitation im Verhältnis zur elektrischen Wechselwirkung und starken Wechselwirkung liegt in der falschen Annahme begründet, daß es generell einen Masse entkoppelten Raum gibt. Berücksichtigt man den Raum, den makroskopische Körper sowohl durch ihre Objektausdehnung als auch durch ihren Wechselwirkungsradius aufspannen, dann wird deutlich, daß die "fehlende" Energie in dem Raum selbst "steckt". In diesem Sinne ist für makroskopische Körper die Gravitationskonstante γG das »Maß der Dinge«.

 

Makroskopische Körper und Gravitation

Für Körper mit von rG/mG abweichenden Radius-Masse-Verhältnissen bedeutet dies umgangssprachlich schlicht, daß "Arbeit" verrichtet werden musste, um einen größeren (Körper-)Raum aufzuspannen, als er im längenkleinsten, massereichsten Elementarquant {G} natürlich-kodiert vorliegt. Unter Berücksichtigung der Energie-Erhaltung kann diese Energie nur aus der masseabhängigen Ruhe-Energie stammen. In der masseabhängigen Wechselwirkung der Gravitation kommt dann nur der Masseanteil (effektive Masse) zu tragen, der nach Abzug der Masse äquivalenten Raum-Energie zur Verfügung steht. Bereits an dieser Stelle wird deutlich, wie "fantastisch" einfach Gravitation zu verstehen ist, wenn eine entsprechend einfache Denkmodell-Phänomenologie vorliegt. 

Bekannte makroskopische Objekte (...Billardkugel, Fußball, Erde, Sonne,...) genügen offensichtlich nicht der Masse-Radius-Konstantengleichung. Ihre reale Ausdehnung ist (schon vor der Wechselwirkung) um viele Zehnerpotenzen größer, als es Gleichung [F1] masse-radius-gekoppelt für Elementarkörper fordert.

 

 

Darüber hinaus ist das Objekt-Radius-Masse-Verhältnis (RO/MO) um viele Zehnerpotenzen größer als bei dem maßgebenden Elementarquant. Ohne die konkrete Natur der Vielteilchen-Verschachtelung zu kennen, lässt sich allgemein verstehen, daß die scheinbar im Verhältnis zur Ruhe-Energie fehlende [Raum-]Energie der Gravitationswechselwirkung in der realphysikalischen Objekt-Ausdehnung steckt, welche durch den Objektradius rO bzw. durch den Wechselwirkungs-Abstand r (Wechselwirkungsradius) zum Massenschwerpunkt gegeben ist.

 

Die Raum-Energie ER berechnet sich zu :

Praktische Festlegung   Mit der Annahme, daß das Elementarquant {G} der längenkleinste und inhärent massereichste Einzelkörper ist, ergibt sich, daß hier der Raumenergie-Nullpunkt vorliegt. Das bedeutet, daß alle Werte-Angaben zur Raum-Energie ER  Gleichung [ER] additiv auf diesen Nullpunkt der Raum-Energie bezogen sind.

 

 

 

Daraus folgt die effektive Wechselwirkungs-Masse Meff =  (rG/r)·mx , diese wird indirekt durch die Gravitationskonstante im Newtonschen Gravitationsgesetz ausgedrückt. Die der effektiven Wechselwirkungsmasse äquivalente gravitative Selbst-Energie lässt sich (auch) aus der radius-masse-gekoppelten Energie des Elementarkörpers (vergleiche Gleichung [E1r]) ableiten, wenn man die "Skalierung" mittels rG/RO berücksichtigt.

 

Aus diesen simplen Plausibilitätsbetrachtungen folgt, daß Gravitation, auf Grund der Phänomenologie eines energieerhaltenden, masse-radius-gekoppelten Raumes, im Rahmen einfachster Mathematik formal-analytisch erfassbar ist. Im (Wunsch-)Denken hypothetischer Gravitonen handelt es sich vorliegend - plakativ formuliert - "aber nur" um einen austauschteilchenlosen Skalierungseffekt. Die innere räumliche Zusammensetzung und Verschachtelung der atomaren- oder molekularen Struktur der makroskopischen Vielteilchenobjekte hat keinen Einfluss auf die Gravitationskraft respektive Gravitations-Energie, solange der Wechselwirkungsradius r größer ist als der Objektradius RO ( r > RO  =  "elastische Wechselwirkung").

 

Selbstähnlichkeit

"Intuitiv-spielerisch" ist die Annahme, daß das Verhältnis von zeitabhängigen Universumsradius zu zeitabhängiger Universumsmasse zeitunabhängig (!) ist. Die Multiplikation von ( rUni/mUni ) mit c² ist gleich der Gravitationskonstanten γG. Diese Annahmen stellen u.a. eine "schöne" Korrespondenz zwischen Kosmos, Gravitationskonstante und dem Elementarquant { : G mit rG, mG } respektive den Planckgrössen für Masse (mPl) und Länge rPl (Radius) her. Diese Annahmen führen zu konkreten Berechnungen, wie der maximalen Universumsmasse, dem maximalen Universumsradius und mit Hilfe der Wasserstoffparameter (Elektron-, Proton-Masse und Grundzustandsenergie) zur Berechnung der Temperatur der Hintergrundstrahlung, siehe exemplarisch das Kapitel Hintergrundstrahlung.

Randnotizen: Schon Ernst Mach (1838 - 1916) bemerkte, daß die "Schwäche" der Gravitation mit der "enormen" Grösse des Universums in Zusammenhang steht. Er vermutete eine Relation zwischen Universums-Masse, Universums-Radius und Gravitationskonstante. Sir Arthur Stanley Eddington (1882 - 1944) erhielt das Verhältnis von Universums-Radius zu Universums-Masse indem er die Gravitationskonstante durch c² dividierte (...formal-gleich im Rahmen der hier beschriebenen Korrespondenz zwischen "Längen-Kleinsten" und Längen-Größten"). Und auch Erwin Schrödinger hatte dies als Möglichkeit bereits 1925 geäußert. Quelle: Mach’s Principle – Relating Gravity to the Universe

Warum sich diese einfache Annahme nicht durchsetzte hat höchstwahrscheinlich mit der (später) favorisierten (inflationären) Urknalltheorie zu tun. Dort ist kein Platz für "(korrespondierend) Einfaches".  

 

Fazit: Obige Basisanalyse der Gravitation entzaubert diverse Mythen (Stichworte: Graviton,  Dunkle Energie, Dunkle Materie) zur Universumsbildung. Offensichtlich kann man - salopp formuliert - vorliegenden "Skalierungseffekt" denkmodell-basierend nicht noch einfacher gestalten. Weder "ART-übliche" differentialgeometrische Betrachtungen, Überlichtgeschwindigkeit und vierdimensionale Raum-Zeit-Konstruktionen sind notwendig. Ganz im Gegenteil, die omnipräsente Mathematik-Gläubigkeit und Mathematik-Fokussierung haben offensichtlich den Blick für erkenntnistheoretisch wertvoll "Einfaches" verbaut. Des Weiteren lässt sich die hier beschriebene "gravitative" Wechselwirkung phänomenologisch nicht mit der Quantenfeldtheorie (QFT) "vereinheitlichen", da es gar keine Notwendigkeit gibt, dies zu tun. Die postulierten "Austauschteilchen-Objekte" des Standardmodells der Teilchenphysik (SM), sprich Gluonen und Vektorbosonen und im weitesten Sinne Neutrinos "koppeln" nicht an die Gravitation, selbst wenn diese "Kräfte-Vermittler" existieren würden. Ohne das an dieser Stelle explizit auszuführen, existieren aber weder Gluonen, Vektorbosonen noch Neutrinos (siehe dazu die Kapitel Standardmodell und Neutrinos).

 

Übrigens: Der reale Erfolg einer Theorie lässt sich durchaus objektiv-praktisch bewerten, um es mit den Worten Michael Köhlers auszudrücken: “Prüfstein für Spekulationen und Hypothesen kann nur das Experiment  und - wo dieses angesichts unmenschlicher Zeiten und Weiten unmöglich wird - nur die  Beobachtung der Natur sein. Letztlich werden auch kosmologische Erkenntnisse erst dann zur praktischen Gewissheit, wenn sie in Synthesen einfließen, in technischen Lösungen genutzt werden." In diesem Sinne ist die Newtonsche Gravitationstheorie (nach wie vor) mit Abstand die praktisch erfolgreichste.  

 

 

weitere Betrachtungen

Was ist und was darf sein?

Nicht nur populärwissenschaftlich, sondern auch fachlich "reden und philosophieren", Standardmodellfreunde von Schwarzen Löchern und Größen, wie dem Schwarzschildradius, überzeugt und beratungsresitent wie Strenggläubige bezüglich ihrer eigenen historischen Schriften.

 

Schwarzschildradius und (formale) Bedeutungsproblematik

Das Grundproblem der inhaltlichen Bedeutung - und der in der Literatur mehr oder weniger beliebigen Bedeutung - des Schwarzschildradius rS, ist tief verwurzelt mit dem mathematischen Formalismus der Allgemeinen Relativitätstheorie (ART). Siehe exemplarische Ausführungen von Dr.Ralph Hübner1 zum Metrischen Tensor (Seite 92), dort insbesondere das Ergebnis (7.17). 1[ Vom Basiswechsel zum Urknall, eine Einführung in die Allgemeine Relativitätstheorie]

Im Innenbereich des Schwarzen Lochs besitzt die radiale Komponente den Charakter einer Zeit (!). Dort berechnet sich der Schwarzschildradius gemäß Gleichung 7.87 (Seite 104) zu (π/2)rS1. Im Rahmen der Elementarkörpertheorie entspricht das der Elementarkörper inhärenten Wellenlänge, die der Compton-Wellenlänge λC(MS(rS)) der Masse MS entspricht.

 

Metriken, Schwarze Löcher und ihre Bedeutung(slosigkeit)

Die Gleichungssysteme (Einstein, Friedmann) der Allgemeinen Relativitätstheorie (ART) liefern keine analytischen Lösungen. Erst Idealisierungen und Näherungen führen begrenzt zu rechenbaren Lösungen. Die (kovarianten) Widersprüche kommen mit den offensichtlich unzulässigen Idealisierungen und Näherungen. Denn mathematisch kann das Kovarianzprinzip gar nicht „verletzt“ werden, da es axiomatisch begründet ist. Nur diese axiomatische Voraussetzung „entschwindet mit der Verstümmelung“ (Idealisierung und Näherung) der eigentlichen Gleichungen. Mit anderen Worten: Die mathematisch korrekten Gleichungen besitzen keine analytischen Lösungen. Die reduzierten Gleichungen (Näherungen, Idealisierung) besitzen zwar Lösungen, diese sind jedoch nicht kovariant. Somit besitzt keine Lösung eine realphysikalisch begründete Bedeutung. Diese Art des Mathematikgebrauches ist willkürlich, da je nach „Geschmack“ der (selbst)gewählten Metrik andere Ergebnisse erhalten werden.

In der üblichen "physikalischen Auswertung" des Linienelementes ds² der Schwarzschild-Metrik der ART wird eine Nullstelle bzw. Polstelle als Schwarzschild-Radius interpretiert. In einer mehr oder weniger assoziierten Plausibilitätsbetrachtung wird danach gefragt, ab welcher Entfernung Photonen/elektromagnetische Wellen im Feld einer "gravitierenden Masse" energetisch nicht mehr entweichen können.

Die Eddington-Finkelstein-Koordinatentransformation beseitigt die Koordinatensingularität der Schwarzschildlösung "sorgt" aber auch dafür, daß für die "avancierte" Lösung nach innen und für die "retardierte" Lösung nach außen Teilchen ins Schwarze Loch eindringen und austreten können !  Mit anderen Worten: Die postulierten Schwarzen Löcher der Ur-Version der Schwarzschild-Metrik waren bei genauer Betrachtung das Resultat zweier Integrationskonstanten eines beliebig gewählten Koordinatensystems. Ein weiteres Koordinatensystem der Herrn Eddington und Finkelstein behebt das Koordinaten-Artefakt, "bringt" dem vermeintlich Schwarzen Loch aber nun die Eigenschaft, daß Teilchen das Schwarze Loch verlassen können.

Mit anderen Worten, die Schwarzen Löcher der "einen" Metrik, sind keine Schwarzen Löcher der "anderen" Metrik.  

Noch einige Worte zu einem Hauptproblem der ART und allgemein zu theoretischen Ansätzen...

Die »thermodynamische Unverträglichkeit«

1..."Sowohl Stephen Hawking als auch Sir Roger Penrose kümmern sich auffällig wenig um zeitgenössische Thermodynamik! Ihr diesbezügliches Weltbild endet bei Boltzmanns früh gescheitertem Versuch, die mechanistische Tradition der Lagrange-Hamiltonschen Theorie in der Thermodynamik zu verankern. Dafür gibt es einen schier untrüglichen Beweis: In keinem ihrer Bücher wird auch nur einmal der Name desjenigen Gelehrten erwähnt, der nicht nur die Thermodynamik, sondern letztlich durch seine Elementary Principles in Statistical Mechanics auch die Quantentheorie vom Kopf auf die Füße gestellt hat: Der US-amerikanische Eisenbahn-Ingenieur und erste Doktorin-genieur in den USA und spätere Yale-Professor Josiah Willard Gibbs (1839 - †1903). Ein solcher Fehler ist nicht nachvollziehbar!...

1...die Fata Morgana: die Verbindung zwischen Information und Entropie. Zwei Worte, die man – laut John von Neumann  – beide nicht versteht, werden durch einen Logarithmus und eine dimensionsstiftende Konstante miteinander verknüpft. Was noch mehr verblüfft: Viele Kosmologen glauben allen Ernstes, dadurch die Thermodynamik und deren ganzen begrifflichen Apparat mit ins Boot zu holen. Daher Hawkings ‚Logik’: „Das Problem in Bekensteins Argumentation war, dass ein Schwarzes Loch, besäße es eine endliche Entropie proportional zur Fläche seines Ereignishorizonts, auch eine endliche Temperatur haben müsste. Daraus würde folgen, dass sich ein Schwarzes Loch bei irgendeiner Temperatur ungleich Null mit der thermischen Strahlung im Gleichgewicht befinden könnte. Doch nach klassischen Begriffen ist kein solches Gleichgewicht möglich, da das Schwarze Loch… absorbieren würde, ohne… zu emittieren.“ [HAWKING, S. W. (1998), S. 103].

1...Was die internationale Elite der theoretischen Kosmologen nie zur Kenntnis genommen hat – weil ihre Nachwuchsleute bei der vielen Konkurrenz wahrscheinlich nie Gibbs’ Hauptwerke studiert haben – war die simple Tatsache, dass ‚ihre Entropie’ eher eine 'Shannonsche Entropie' ist, nämlich Informationen betreffend, indes keine thermodynamische Entropie. Somit ist sie keiner absoluten, d.h. thermodynamischen Temperatur konjugiert. Folglich existiert auch kein Problem mit einer thermischen Strahlung. Natürlich steht es jedermann frei – wie Bekenstein und Hawking – Formeln für ‚ihre Entropie und Temperatur’ z. B. aus dem ›Ereignishorizont‹ ‚abzuleiten’. Nur mit der Systemtheorie nach Gibbs, Falk u. a. hat das alles nichts zu tun! Dort ist die Entropie eine ›Allgemeinphysikalische Größe‹ mit eigenständiger Bedeutung, die Temperatur T nichts anderes als die partielle Ableitung (∂E/∂S )A, B, C…bei konstant gehaltenen ‚aktiven’ ›Allgemeinphysikalischen Größen‹ A, B, C … des betreffenden Systems. Zudem sind die Hauptsätze der Thermodynamik und die daraus abgeleiteten Bewegungsgleichungen mit Prozessgrößen formuliert, die lokal nichts mit der Einstein-Geometrie der ART zu tun haben. Das führt sofort zum Problem, inwieweit der Zweite Hauptsatz überhaupt mit der ART kompatibel ist...

1...Wenn man unbedingt eine zur Information konjugierte 'informelle Temperatur' will, muss man sie aus der 'Informationstheorie' ableiten; gewiss hat sie aber nichts mit der Kelvintemperatur zu tun und somit schon gar nichts mit physikalischen Strahlungsprozessen...

1...Das ‚Urknall-Problem’ als ‚Ur-Singularität’ tritt theoretisch nur dann auf, wenn Einsteins Credo (: Irreversibilität sei eine Illusion) zutrifft. Dieser Schluss bedeutet dann aber, dass man die Thermodynamik von vorneherein konsequent negiert und sich auf die lupenreine Hamilton-Mechanik als Basis der ART beschränkt, oder zumindest nur isentrope Prozesse (keine Entropieänderung) ins Auge fasst, um wenigstens das Phänomen der Hintergrundstrahlung zu ‚retten’...

1Quelle: Nichtmechanistische Darstellung der physikalischen Disziplinen als mathematische Systemtheorie   Vilmos Balogh

 

Insgesamt gilt: Natur kann nur addieren oder subtrahieren. Eine „gesicherte“ höhere mathematische Realität existiert ausschließlich im Rahmen axiomatisch begründeter Sprache (Mathematik). Inwieweit eine korrekte mathematische Struktur (höhere mathematische Realität) physikalisch anwendbar ist, lässt sich mit den „Mitteln“ der Mathematik nicht entscheiden (siehe „unstrittig-exemplarisch“ Epizykeltheorie und Banach-Tarski-Paradoxon).

 

 

 

Es gibt beispielsweise keine physikalische Grundlage für die Herleitung der Feldquantisierung. Quantenfeldtheoretische Betrachtungen sind „realobjektbefreite“ mathematische Denkmodelle. Mathematik erfasst letztendlich Mengen und kann nicht unterscheiden zwischen Staubsauger und Staub. Mathematik ersetzt keine Phänomenologie. Das Schwarze Löcher spektakulärer sind als keine ist eine massenpsychologische Entscheidung, so zu tun als ob sie physisch mit Sicherheit existieren, ist unbegründet.

Zur Erinnerung: Schon Theodor Fontane beklagte Ende des 19.Jahrhunderts den Untergang der Denkkultur mit den Worten:

»Wir stecken bereits tief in der Dekadenz. Das Sensationelle gilt, und nur einem strömt die Menge noch begeisterter zu, dem baren Unsinn.«

 

 

Unbegründete Feldenergie

Das Gravitationsfelder selbst eine physikalische Realität besitzen und über ein unendliches Energiereservoir verfügen sollen, ist alles andere als "naheliegend". Insbesondere unter der Berücksichtigung, daß der Energieerhaltungssatz gelten soll. Bei Verwendung unendlicher Energiereservoirs in Form von postulierten Feldern erübrigt sich die Frage der Energieerhaltung als Auswahlkriterium für Denkmodelle. Mit dem postulierten Feld kommt die Beliebigkeit. Die Idee eines stets vorhandenen (instantan) wirkenden Feldes lässt offensichtlich mathematische Berechnungen zu, aber es macht phänomenologische Betrachtungen unmöglich.

Merke: Das („klassische“) Feld ist ein Märchen. Denn dieses wäre energetisch für jede noch so kleine Masse unendlich, sowie für jede Ladung. Jeder realphysikalische Körper hat eine endliche Ausdehnung, er ist von diskretem Ausmaß. Verringert sich der Wechselwirkungsabstand und wird dieser kleiner als der Objektradius kommt es phänomenologisch zu einer inelastischen Überlagerung der inneren Strukturen der Wechselwirkungspartner. In diesem Zusammenhang divergiert nichts. Die "Renormierungs- und Regularisierungs-Versuche", initial ausgehend von der Quantenelektrodynamik, des quantisierten Feldes sind notwendige mathematische Hilfskonstruktionen einer ursächlich falschen Phänomenologie. Divergenz (der Felder) ist somit realphysikalisch ausgeschlossen. Plausible Phänomenologie bedarf "Neuen Denkens".

Neues Denken  Neue Physik

Das Geheimnis der "scheinbar" sehr schwachen Gravitation im Verhältnis zur elektrischen Wechselwirkung und starken Wechselwirkung liegt in der falschen Annahme begründet, daß es generell einen Masse entkoppelten Raum gibt. Berücksichtigt man den Raum, den makroskopische Körper sowohl durch ihre Objektausdehnung als auch durch ihren Wechselwirkungsradius aufspannen, dann wird deutlich, daß die "fehlende" Energie in dem Raum selbst "steckt". In diesem Sinne ist für makroskopische Körper die Gravitationskonstante γG das »Maß der Dinge«. Aus der Gravitationskonstanten lässt sich ein Körper {Elementarquant G} konstruieren, der sowohl die größtmögliche Einzelmasse {mG} vorgibt, als auch einen "natürlich" Masse gekoppelten inhärenten Körperradius {rG}.

Für Körper mit von rG/mG abweichenden Radius-Masse-Verhältnissen bedeutet dies umgangssprachlich schlicht, daß "Arbeit" verrichtet werden musste, um einen größeren (Körper-)Raum aufzuspannen, als er im längenkleinsten, massereichsten Elementarquant {G} natürlich-kodiert vorliegt. Unter Berücksichtigung des Energie-Erhaltungssatzes kann diese Energie nur aus der masseabhängigen Ruhe-Energie E0 stammen. In der masseabhängigen Wechselwirkung der Gravitation kommt nur der Masseanteil (effektive Masse) zu tragen, der nach Abzug der Masse äquivalenten Raum-Energie zur Verfügung steht. [Weiter unten werden dazu explizite Berechnungen durchgeführt.] Mit dieser Annahme wird die vermeintliche "masseabhängige Schwäche" der Gravitation makroskopischer Körper erklärbar. Das es sich im Gravitationsgesetz [EG1] bei makroskopischen Körpern um verschachtelte n-Vielteilchen-Objekte handelt, deren Anzahl n sich durch das Verhältnis von Körpermasse zu Elementarquantmasse (mx/mG = nmG / mG = n) definiert, wird ebenfalls weiter unten explizit ausgeführt. Die Elementarkörper basierende makroskopische Gravitationswechselwirkung ist so geartet, daß die konkrete Verschachtelungsstruktur keinen Einfluß auf die Wechselwirkungsenergie in Abhängigkeit des Wechselwirkungsradius r hat, wenn r ≥ rO ist.

 

Experimentelles

derzeit [Aug.2018] genaueste Bestimmung von γG

Physicist Shan-Qing Yang of Huazhong University of Science and Technology in Wuhan , China , and colleagues measured G using two instruments called torsion pendulums...

These torsion pendulum experiments yielded γG values of 6.674184e-11 and 6.674484e-11 m3s-2kg-1, both with an uncertainty of about 0.00116 percent.

            

 

Elementarkörpertheorie basierende Ergebnisse

Die vermeintlich geringe Stärke der makroskopischen Gravitation ist darauf zurück zu führen, daß in der Betrachtung und Berechnung die Raumausdehnung der makroskopischen Körper nicht berücksichtigt wird. Elementarkörpertheorie basierend gibt es aber keinen Materie ( : Masse, respektive Energie) entkoppelten Raum. Dies wird nicht "wahrgenommen", da der Raum und somit die radius-abhängige Energie der makroskopischen Systeme phänomenologisch von der "etablierten" Physik nicht "realisiert" wird. Dieser fatale Irrglaube war und ist u.a. notwendig, um die überlichtschnelle masse-entkoppelte Raum-Expansion des "frühen" Universums während der so genannten Inflationsphase des Urknall-Modells zu rechtfertigen.

 

Merke: Ein leerer Raum kann keine physikalischen Eigenschaften besitzen. Mit der Einführung eines solchen Raum-Feld-Begriffes kann man insbesondere nichts dynamisch erklären. Masse entkoppelter Raum existiert nicht und ist keine Energie-Quelle.

Raum ist eine Energieform.

Wenn wir makroskopisch Raum vorfinden, dann wurde dieser mikroskopisch von masse-radius-gekoppelten Elementarkörpern gemäß [F1] und [E1r] generiert.

Es gibt eine einfache Masse-Radius-Beziehung [F1], die alle Elementarkörper verbindet.

Am "Rande bemerkt" Mit Gleichung [F1] lässt sich einfachst der Protonenradius berechnen

Das Produkt aus Protonenmasse und Protonenradius ist nur von Naturkonstanten abhängig. Mit Kenntnis der Protonenmasse ergibt sich der Protonenmasse inhärente Protonenradius.

[ http://www.psi.ch/media/proton-size-puzzle-reinforced ]

[ http://www.psi.ch/media/weiter-raetsel-um-das-proton ]

»updates«

6.Oktober 2017 und März 2018

Eine weitere experimentelle Bestätigung der Elementarkörpertheorie-Voraussage zur Grösse des Protonenradius

rp(EK-Theorie) = 8,41235642 · 10-16 m

rp(CODATA)  = 8,751(61) · 10-16 m

Wissenschaftler am Max-Planck-Institut für Quantenoptik bestätigen mit hochpräziser Laserspektroskopie an regulärem Wasserstoff den unerwartet kleinen Protonenradius von myonischem Wasserstoff rp(μ) = 8,4087(39) · 10-16 m.

Es ergeben sich folgende Werte für die Rydberg-Konstante und den Protonenradius für regulären Wasserstoff

R∞ = 10973731.568076(96) m-1

rp = 8,335(95) 10-16 m

Quelle: https://www.mpq.mpg.de/5557257/17_10_06

... weitere Details siehe Originalveröffentlichung:  

The Rydberg constant and proton size from atomic hydrogen
Science, 6 October 2017, DOI:10.1126.science.aah6677

und Details zum Meßverfahren ...

Dissertation  The Rydberg Constant and Proton Size from Atomic Hydrogen Axel Beyer 2016

 

Helmholtz-Preis 2018 für Axel Beyer und Lothar Maisenbacher

Mit neuen Experimentiermethoden schafften es die Garchinger Physiker, die Frequenz des 2S-4P-Übergangs in Wasserstoff auf 2.3 kHz genau zu bestimmen, was einer relativen Messungenauigkeit von 4·10-12 entspricht.

Diese Messung ist fast so genau wie alle anderen bisherigen Experimente an regulärem Wasserstoff zusammengenommen. Die daraus abgeleiteten Werte für die Rydberg-Konstante und den Protonenradius stimmen sehr gut mit den Messungen an myonischem Wasserstoff überein…

 

 

Elementarkörper spannen (erst) den radialsymmetrischen "Raum" auf, der als solcher in Gestalt von Kugeloberflächen "natürlich" gekrümmt ist. Die Physik spielt sich auf einer oszillierenden Kugeloberfläche ab. Somit ist der dreidimensionale Raum (mikroskopisch) eine Superposition von zweidimensionalen Kugeloberflächen und in der Wechselwirkung kontinuierlich. Wenn man so will, verkörpern dynamische Oberflächen das "Feld". Die Tatsache, daß elementare Strukturen aus oszillierenden Kugeloberflächen bestehen, führt zu einer konstruktiven „Beschreibungsverarmung“. Die Isotropie führt zu einer 2-dimensionalen Plausibilität, die sich formal auf Zeit und Radius „verarmt“. Die Selbstverständlichkeit, daß die Wegstrecke auf einer Kugeloberfläche nicht der euklidischen Entfernung zwischen den Punkten A und B entspricht bedarf keiner Abstraktion. Daraus ergibt sich Elementarkörper basierend die Compton-Wellenlänge λC als Masse-Äquivalent. "Glücklicherweise" lässt sich in erster Näherung die Wechselwirkungs-Physik ohne Berücksichtigung der inneren dynamischen Struktur berechnen.

Der Raum, der von Elementarkörpern aufgespannt wird, enthält die "verborgene" Energie, diese steckt in der räumlichen Ausdehnung. Die Superposition führt letztendlich zur makroskopischen Gravitation. Bekannte makroskopische Objekte (...Billard-Kugel, Fußball, Erde, Sonne,...) genügen nicht der Masse-Radius-Konstantengleichung. Ihre reale Ausdehnung ist um viele Zehnerpotenzen größer, als es Gleichung [F1] für Elementarkörper fordert. Ohne die konkrete Natur der Vielteilchen-Verschachtelung zu kennen lässt sich jedoch allgemein verstehen, daß die scheinbar im Verhältnis zur Ruhe-Energie fehlende Energie der Gravitationswechselwirkung in der Ausdehnung steckt, welche durch den Objektradius rO bzw. durch den Abstand r zum Massenschwerpunkt gegeben ist. Dies wird weiter unten qualitativ und quantitativ ausgeführt.

 

 

Herkunft und Bedeutung der Gravitationskonstanten γG

"Die" Gravitationskonstante γG ist aus dem Verhältnis von Elementar-Körper-Radius rG zu Elementar-Körper-Masse mG multipliziert mit der Lichtgeschwindigkeit zum Quadrat gegeben γG=(rG/mG)c² :

                                                   

D.h., die im "bekannten" Gravitationsgesetz verwendete Gravitationskonstante γG bezieht sich auf den "längen-kleinsten" Körper G. Dieser Sachverhalt ist nicht offensichtlich, da das Gravitationsgesetz [GE1] im formalen Ergebnis diesen ursprünglichen Zusammenhang nicht explizit offenbart.

 

grenzüberschreitende Bedeutung des Elementarquants... 

Die außergewöhnliche Bedeutung des Elementarquants ist grenzüberschreitend und führt vom Mikrokosmos zum Universum. Teilt man die geschätzte Masse des Universums in der Größenordnung von 1053 [kg] durch die Elementarquantmasse von 10-08 [kg], so ergibt sich ein Verhältnis von 1061. Teilt man den Radius des Universums in der Größenordnung von 1026 [m] durch den Radius des Elementarquants von 10-35 [m] so ergibt sich ebenfalls ein Verhältnis von 1061.

 

 

 

Positive und negative Energien

Des Weiteren leitet sich die Newtonsche Gravitationsenergie EG der Massen m1 und m2, wie im Fall der Masse-Energie-Äquivalenz (Einstein und Dirac),

 

ursprünglich aus der quadratischen "Gravitations-Energie-Gleichung" [EG1] ab :

Das mag erst einmal beliebig und banal erscheinen. Im Rahmen der Elementarkörpertheorie sind negative und positive Energiewerte jedoch evident.

 

 

 

Planckmasse mPlanck und Plancklänge rPlanck

Gibt es so etwas wie den (längen-)kleinsten, genauer radius-kleinsten Körper? Wenn ja, welche Randbedingungen gelten? Bemerkenswert ist das Ergebnis. Auch unabhängig von der Elementarkörpertheorie führt im Rahmen der etablierten Physik die kleinste "physikalische" Länge, die so genannte Plancklänge zu einer im Vergleich  "riesigen" Masse, der so genannten Planckmasse. Bis auf den Faktor 4 = 2 x 2 "bestätigt" die "etablierte Physik", verkörpert durch die Planck-Masse und Planck-Länge, die Masse-Radius-Konstantengleichung [F1].

 

 

Dimensionsanalyse von Max Planck

Beginnen wir mit der einstigen Herleitung der Planckgrössen. Die von Max Planck (1858 - 1947) Ende des 19.Jahrhunderts, Anfang des 20.Jahrhunderts eingeführten Planckgrössen ergeben sich "unphysikalisch" aus einer dimensionsanalytischen Betrachtung der Gravitationskonstanten. Es werden die Einheiten der Gravitationskonstanten: m³ s-2 kg-1 , der Lichtgeschwindigkeit: m s-1 und des Planckschen Wirkungsquantums: kg m  m s-1 , der Länge l, der Masse m und der Zeit t zugeordnet und dann durch Quotientenbildung und Vergleich die Beziehungen hergestellt.

 

 

In jedem Fall bestätigt die "Planck-Skala" die Masse-Radius-Konstantengleichung [F1] der Elementarkörpertheorie. Denn das Pendant zur "winzigen" Plancklänge ist die "riesige" Planckmasse, so wie es die Theorie voraussagt.

Warum Planck nun für hx = h/2π wählte ergibt sich nicht aus der Dimensionsanalyse.

Das Max Planck offensichtlich die phänomenologische Bedeutung nicht erkannte und letztendlich nicht realisierte, daß aus energetischen Gründen (siehe weiter unten) nur die doppelte Planckmasse und nur die doppelte Plancklänge als maximale bzw. minimale  Einzelkörper-Dimensions-Grenze in Frage kommt, ändert nichts an der grundsätzlichen Masse-Raum-Kopplung der Planckgrössen.

 

Aus der Gravitationskonstanten lässt sich somit ein Körper {Elementarquant G} konstruieren, der sowohl die größtmögliche Einzelmasse {mG} vorgibt, als auch einen "natürlich" Masse gekoppelten inhärenten Körperradius {rG}.

        

 

 

Planckladung qPlanck

Die Planckladung ergibt sich aus Vergleich der elektrischen Energie mit der masse-radius-gekoppelten Gesamtenergie.

                                 

 

Wie im Fall der  Planckmasse mPlanck und Plancklänge rPlanck ist das Maß der Dinge aus energetischen Gründen nicht die Planckladung, sondern die doppelte Planckladung, dessen Grösse in Anlehnung an das vorliegende Elementarkörper-Denkmodell suggestiv (starke) Elementarkörper-Ladung q0 genannt wird. Aus obiger Herleitung ergibt sich die Sommerfeldsche Feinstrukturkonstante α als sekundäre Grösse der primären Grösse der elektrischen Elementarladung e. Das energetische Maß ist in diesem Sinne nicht α sondern α/4 und gibt das Verhältnis von elektrischer zu masse-radius-gekoppelter Gesamtenergie an.

Weiterführendes

Mit den beiden "Ladungstypen" e und q0 lässt sich die gesamte Materie als Wechselwirkungsfolge der Proton-Elektron-Kopplung entwickeln.

 

 

 

 

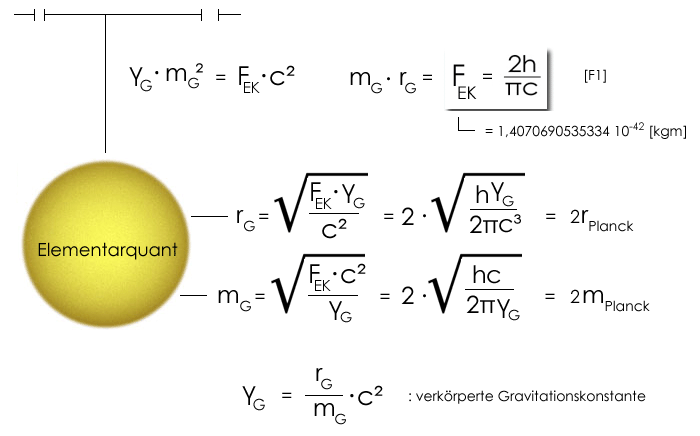
Klassische Betrachtung*

*es folgt im Anschluss an die Klassische die Allgemeine (Relativistische) Betrachtung

 

Klassische Beschreibung und Berechnung der zur Gravitationsenergie EG inhärenten Raum-Energie ER

 

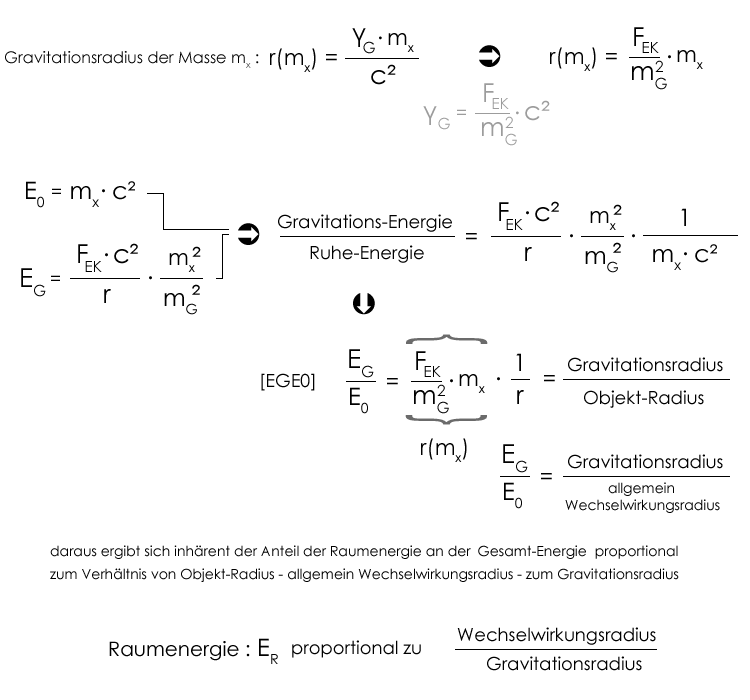
Das Gravitationsgesetz ist auf den längen-kleinsten Körper {G} normiert !

Nur wenn ein makroskopischer Körper der Masse mx einen Radius besitzen würde, der dem Gravitationsradius rxG(mx) entspricht, dann ist die Gravitations-Energie EG gleich der Ruhe-Energie E0 = mxc². Mit der Elementarkörpertheorie basierenden Annahme, daß eine Vergrößerung des (Objekt-)Radius masse-gekoppelte Energie in Raum-Energie ER transformiert, wird plausibel, daß die Gravitations-Energie, die ausschließlich die masse-gekoppelte Energie E(mx) berücksichtigt um die Raum-Energie reduziert ist. Da makroskopische Objekte um viele Zehnerpotenzen größer sind, als ihr Gesamtmasse zugehöriger Gravitationsradius, steckt fast die gesamte Energie (bezogen auf die Ruhe-Energie E0 in dem vom »Objekt« aufgespannten Raum bzw. in dem Raum mit Wechselwirkungsradius r.

 

Berechnung der Raumenergie ER makroskopischer Körper      Klassischer Fall

Praktische Festlegung   Mit der Annahme, daß das Elementarquant {G} der längenkleinste und inhärent massereichste Einzelkörper ist, ergibt sich, daß hier sozusagen der Raumenergie-Nullpunkt vorliegen soll. Das bedeutet, daß im klassischen Fall alle Werte-Angaben zur Raum-Energie ER auf diesen Nullpunkt der Raum-Energie bezogen sind.

Mit dieser Festlegung lässt sich nun für alle makroskopischen Körper mit mx » mG die Raum-Energie ER berechnen :

 

Der Wechselwirkungsradius r (≥ rO) kann, so wie der Objektradius rO , direkt mit der Masse mx assoziiert werden. Das bedeutet, daß sich die Raum-Energie allgemein auf den aufgespannten Raum bezieht. Um eine Vorstellung von der "Größe" der Raum-Energie zu bekommen, folgen einige Rechenbeispiele "diskreter" Objekte.

Der Literaturwert des Universums von 4,26·1026  [m] ist stark theoriebeladen (inflationäres Urknall-Modell) und "schlicht" falsch. Eine Elementarkörpertheorie basierende Berechnung fördert eine bemerkenswerte Korrespondenz zu Tage. (Details siehe das Kapitel Urknall & Universum)

Das bedeutet, daß lokal zwar die Gravitationsenergie  - auf Grund der inhomogenen Masseverteilungen und deren Verhältnisse von Objektradius zu Gravitationsradius -  im Verhältnis zur Ruhe-Energie, wie beschrieben und experimentell bestätigt ,"sehr klein" ist, aber das Vielteilchen-Gesamtsystem des Universums das gleiche Radius zu Masse Verhältnis aufweist, wie der längenkleinste Einzel-Körper (Elementarquant). Somit ist die gravitative Selbst-Energie des Universums gleich der Ruhe-Energie des Universums.

 

 

Obige "Abschätzung" der Raum-Energie des Universums gemäß Gleichung [ER] ist ein gutes Beispiel für die grundsätzliche Problematik eines mathematisch-formalistischen Ansatzes. Denn das Universum ist auch in Näherung keine "diskrete", homogene Entität. Ganz im Gegenteil: Massenansammlungen unterschiedlichster Grösse koppeln asymmetrisch inhärente Raumstrukturen. Im Ergebnis kommt es zu dynamischen Prozessen, die lokal Gleichgewichtszustände generieren können (Sonnensysteme, Galaxien). Es stellt sich die Frage ob das Gesamtsystem »Universum«, trotz der Inhomogenitäten, ein stabiles Gleichgewicht erreichen kann. Eisenkugel, Erde und Sonne sind hingegen Objekte diskreter Grösse, die sich als homogen idealisieren lassen. Das bedeutet, die angegebene Raum-Energie des Universums würde nur gelten, wenn das Universum ein Körper wäre, was nicht der Fall ist.

Bekanntes Beispiel eines lokalen Gleichgewichtszustandes : Es ergibt sich die Bahngeschwindigkeit v der Erde um die Sonne durch die Annahme, daß die Erde auf einem vergrößerten "Sonnen-Radius" r ≈ 1,496 1011 [m] (Wechselwirkungsradius: Entfernung Erde-Sonne) kreist. Diese Aussage gilt allgemein auch für andere "Testmassen", da gemäß Gleichung [ER2] die massebehaftete, radiusabhängige Wechselwirkungs-Energie, welche einer effektiven Sonnenmasse im Verhältnis zur Gesamt-Sonnen-Masse, resultierend aus Gesamt-Energie minus Raum-Energie mit Radius r, entspricht.

Insgesamt könnte man "aus Sicht" des » sekundären Begriffes Masse « argumentieren, daß die Oberfläche mit r² wächst und die Masse nicht. Dieser "Sicht" liegt aber eine falsche Annahme zu Grunde. Denn die Masse "verteilt" sich, wie der Radius, zweidimensional. Das wird klar verständlich, wenn man sich die "Substruktur" des makroskopischen Körpers gemäß Masse-Radius-Konstantengleichung [F1] anschaut. Es gilt für Elementarkörper: m0r0 = FEK = const. [F1]  ► reziproke Proportionalität: r0 = FEK/m0

►  r0² = FEK²/m0²   ►  O=O(r0) = 4πr0²  =  4πFEK²/m0².

 

 

 

 

Allgemeine Relativistische Betrachtungen

Integrierte Raum-Energie und Energie erhaltendes Gravitationsgesetz

 

Das Energie erhaltende Gravitationsgesetz stammt von Rudolf Kiesslinger (1921 - 2011)1. Kiesslinger selbst war offensichtlich stark von Ludwig Boltzmanns Arbeiten zur inneren Energie inspiriert.

1Gravitation verknüpft mit Eigenschaften des Lichts 1993/94, 2010

Ohne an dieser Stelle auf eine Fülle von Konsequenzen des Energie erhaltenden Gravitationsgesetzes einzugehen, beginnen wir schlicht mit »Kiesslingers Gravitationsgesetz«. Obwohl Kiesslinger nicht die Raum-Energie explizit erwähnt, existiert eine inhaltliche und formale Schnittmenge mit dem Denkmodell der Elementarkörpertheorie. Kiesslinger folgerte primär, daß die kinetische Energie, ausgehend von Zentralkräften, nicht aus einem postulierten [Gravitations-)Feld, sondern aus der inneren Energie des Körpers stammt. Grenzüberschreitend entspricht das der inneren Dynamik des Elementarkörpers, siehe das Kapitel: Impuls-Masse-Inversion. 

 

Für Abstände r, die groß im Verhältnis zum Gravitationsradius rG ( r » rG ) sind, geht [KIG] über in das Newtonsche Gravitationsgesetz.

 

Herleitung des Energie erhaltenden Gravitationsgesetzes

Kiesslinger definiert die Ruhe-Energie für m0 im Unendlichen ( r = ∞ ) als  E0 = m0c² . Nähert sich nun m0 der Zentralmasse M, so stammt die Bewegungs-Energie der Masse m0 aus der Ruhe-Energie E0. Dies wird durch die noch zu bestimmende Funktion f(r) ausgedrückt. Aus M und m0f(r) ergibt sich eine potentielle Gesamt-Energie Epot = ( M + m0f(r) )c². f ' =df(r)/dr ergibt die Kraft F. Diese ist der Gravitations-Kraft gleichzusetzen. Wobei zu beachten ist, daß auch dort die Masse m0 mit der Funktion f(r) "behaftet" ist. Durch mathematische Umformung ergibt sich f(r) aus f ' / f ...

 

 

Integration des Energie erhaltenden Gravitationsgesetzes führt zur universellen Raum-Energie, so wie diese zunächst als Näherung im klassischen Fall ( Gleichungen [ER2],[ERG],...) angegeben wurde. Kiesslinger selbst hat ausschließlich mit dem Wechselspiel von innerer Energie und kinetischer Energie, ohne Bezug zur Raum-Energie, gearbeitet. Wie jedoch leicht zu erkennen ist, liefert die aus dem Energie erhaltenden Gravitationsgesetz integrierte Energie, die Raum-Energie. Der bereits erörterte klassische Fall endet sozusagen nach dem 2.Glied der Reihenentwicklung der e-Funktion. Daraus folgt, daß die Bewegungs-Energie makroskopischer Körper eine Folge der Änderung der integrierten Raum-Energie ist.

 

 

Aber nochmals: Obige Berechnung der Raum-Energie des Universums gemäß Gleichung [ERA] ist ein gutes Beispiel für die grundsätzliche Problematik eines mathematisch-formalistischen Ansatzes. Denn das Universum ist keine "diskrete", homogene Entität. Die Raum-Energie einer inhomogenen, verschachtelten, dynamischen Überlagerung (ursprünglich primärer Elementarkörper) wird phänomenologisch weder durch Gleichung [ER] noch durch Gleichung [ERA] erfasst.

 

 

 

elementare

Gravitationskonstanten

Der weiterführende Modellgedanke ist, daß in Analogie zum Makrokosmos im Mikrokosmos »Elementarkörper spezifische Gravitationskonstanten« zum erweiterten Energie-Erhaltungssatz [E1r] und zur Ruhe-Energie E0 führen. 

 

Elementare Gravitation und elementares Gravitationspotential

Für einen Elementarkörper mit der Ruhe-Masse m0 und dem Ruhe-Radius r0 ergeben sich somit die Gravitationskonstante γ0 und allgemein das Gravitationspotential Φ zu :

       

 

Multiplikation des Gravitationspotentials Φ(r0,r) mit der Ruhemasse m0 ergibt den erweiterten Energie-Erhaltungssatz :

 

Masse-Radius-Konstantengleichung und erweiterter Energieerhaltungssatz

Das Produkt aus Masse und Radius aller Elementarkörper ist gleich [F1]. Die Erhaltungsgrösse ist also nicht die Masse! Erhalten wird das Produkt aus Masse und Radius.

Erweiterter Energieerhaltungssatz und Gesamt-Energie eines Elementarkörpers

In Analogie zur kinetischen und potentiellen Energie der "klassischen Physik" ist der Ruhe-Radius r0 das Maß für die potentielle Energie und die Ruhemasse m0 das Maß für die Bewegung der oszillierenden Oberfläche. [Details zur inneren Struktur der Elementarkörper siehe:  Impulsmasse-Inversion]

 

 

 

 

Weiterführende Betrachtungen

 

Das es Rudolf Kiesslinger "in sich hat" kann jeder selber unter 1Gravitation verknüpft mit Eigenschaften des Lichts 1993/94, 2010 nachlesen. Kießlinger zeigt u.a., wie eine Erweiterung der "Newtonschen Dynamik" zur Speziellen Relativitätstheorie (SRT) führt. Diese Ausführungen sind durchaus als spektakulär zu bezeichnen.

 

Relativistische Masse-Änderung abgeleitet aus der Newtonschen Dynamik

"Wir benötigen keine über die klassische (Newtonsche) Theorie hinausgehende neue Formulierung, um die Bewegung von Massen relativistisch zu beschreiben." Rudolf Kiesslinger

 

Ergänzend und zum "Vergleich" folgt im Anschluß an Kiesslingers Ausführungen die Elementarkörpertheorie basierende Herleitung des Lorentzfaktors und des dynamisierten Lorentzfaktors. Weder die auf der "Newtonschen Dynamik" basierende Herleitung des relativistischen Faktors, ausgehend von der zeitlichen Änderung des Impulses, noch die Elementarkörpertheorie basierende geometrische Herleitung ist an Inertialsysteme gebunden. 

 

Ableitung der relativistischen Masse  (gemäß Rudolf Kiesslinger)

Folgendes soll gelten: 1.) Masse-Energie-Äquivalenz   2.) Konstanz der Lichtgeschwindigkeit  c = const.  3. Die Axiome von Newton, mit der Erweiterung, daß Massen nicht konstant sind.

Nach Newton ist die Kraft F definiert als zeitliche Änderung des Impulses: F = d/dt (mv). Der entscheidende Unterschied zur Newtonschen Auffassung und somit zur klassischen Physik ist nun die Annahme, daß auch die Masse zeitabhängig ist. Diese Annahme Kiesslingers deckt sich mit den (qualitativen) Aussagen der Elementarkörpertheorie zur inneren Dynamik des Elementarkörpers (...siehe das Kapitel Impuls-Masse-Inversion). Es folgt eine Rekonstruktion Kiesslingers Gedanken. 

Konsequenterweise gilt dann für die Masse-Energie-Äquivalenz [E1], daß diese auch zeitabhängig ist,

      

Für die Energie E entlang der Strecke s mit der Kraft F gilt :

Die nun folgenden mathematischen Umformungen führen zur relativistischen Masse-Änderung in Abhängigkeit der Geschwindigkeit, so wie diese "normalerweise" mittels Lorentztransformation und Postulat der SRT erhalten wird.

Die "Richtigkeit" der nun folgenden Substitutionsgleichung [K09] wird am Ende der Ausführungen bewiesen.

Beweis der Richtigkeit der Substitutionsgleichung [K09] durch Ableitung unter Anwendung der Kettenregel gemäß:

Anmerkung: In der Originalarbeit von Rudolf Kießlinger (siehe pdf-Dokument Seite 23 bzw.Buch-Seite 15) wird, anders als hier dargestellt, eine bestimmte Integration von Gleichung [K07] durchgeführt, die zum Ergebnis [K10] "führen soll". Das erscheint "etwas intransparent". "Alternativ" vorliegende mathematische Umformungen im Anschluß an Gleichung [K07]  finden sich in den Ausführungen zu Kießlingers energieerhaltenden Gravitationsgesetz von Martin Bock. 

 

 

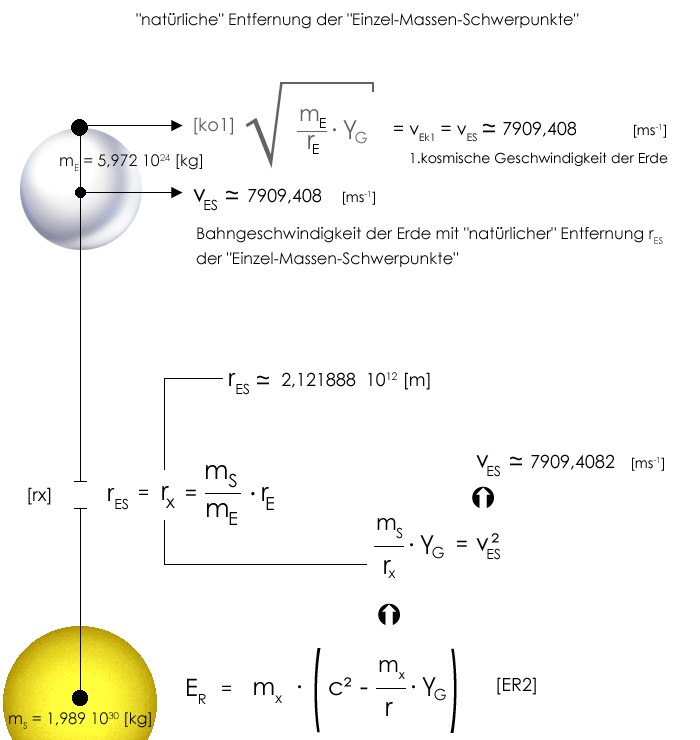
Es folgen noch einige "wenig kontroverse" Ausführungen zur makroskopischen Gravitation.

Natürliches Gleichgewicht und körperspezifische Gravitationskonstanten zweier Körper mit m1, r1 und m2, r2

Unter einem "raum-energetischen" Gesichtspunkt lassen sich »körperspezifische Gravitationskonstanten« γ1 und γ2 einführen:

Wie müsste nun der Radius des Körpers 2 variiert werden, daß energetisch für Körper 1 und Körper 2, in Abhängigkeit der Radius/Masse-Verhältnisse, beide Körper den gleichen Raum-Energie-Anteil besitzen? 

Da hier eine einfache Proportionalität vorliegt folgt:       

rx entspricht dem Abstand der "Einzel-Massen-Schwerpunkte" m1 und m2. Es existiert im Ergebnis ein natürlicher Abstand rx zweier Körper mit den Massen m1 und m2 und den Radien r1 und rx statt r2.

 

Exemplarische Betrachtung aus Sicht der Erde im Hinblick auf die Sonne

"natürliche" Entfernung rES der Einzel-Massen-Schwerpunkte

Für diese Modellrechnung wird die Umlaufbahn der Erde um die Sonne als Kreisbahn idealisiert. Einen Einfluß auf die Kernaussage hat diese Vereinfachung nicht. Mit den Werten mE = 5,972 1024 [kg], rE = 6,371 106 [m] und mS = 1,989 1030 [kg], rS = 6,958 108 [m], wobei der Sonnenradius rS keine Rolle für die weiteren Berechnungen spielt, ergibt sich eine "natürliche" Entfernung der "Einzel-Massen-Schwerpunkte" von rES ≈  2,121888 1012 [m]. Für diesen Abstand gilt, daß die 1.kosmische Geschwindigkeit der Erde vEk1 ≈  7909,408 [ms-1] der Bahngeschwindigkeit vES der Erde um die Sonne entspricht. Es existiert kein weiterer Zustand, der diese "Geschwindigkeits-Gleichheit" aufweist. Salopp könnte man sagen, daß die "natürliche" Entfernung eine korrespondierende Substruktur schafft. 

 

 

 

Das bedeutet, daß das reale Erde-Sonne-Abstandsverhältnis RES ≈ 1,496 1011 [m] nicht die größtmögliche Symmetrie aufweist. Durch den zu rES verkleinerten Abstand  RES  (rES/RES ≈ 14,184) ergibt sich eine reale Bahngeschwindigkeit vES der Erde um die Sonne von ≈  29787,873 [ms-1].

 

    ERDE - MOND interessehalber 

Ohne Berücksichtigung anderer (gravitativer) "Himmelskörper" und ohne Anfangsimpulse, ergibt sich für den Mond (Radius ≈ 1,7375 106 [m], Masse ≈ 7,349 1022 [kg] )  in der Wechselwirkung mit der Erde ( Masse ≈ 5,972 1024 [kg] ) eine natürliche Entfernung von ≈ 1,412 108 [m], mit einer natürlichen (Kreisbahn-)Umlaufgeschwindigkeit von ≈  1680 [ms-1]. Die tatsächliche Entfernung Erde-Mond beträgt jedoch ≈ 3,844 108 [m] mit einer Bahngeschwindigkeit von 1018 [ms-1]. Das bedeutet, der Mond ist ungefähr um den Faktor der Eulerschen Zahl eZ (≈ 2,7182...  als Erinnerungshilfe) weiter von der Erde entfernt, als im natürlichen Zustand.