der Dimensionsanalyse im Rahmen

elementarer Grundstrukturen

Aus dimensionsanalytischer Sicht macht es keinen Unterschied, "wie" formale Ziele erreicht werden. Das grundsätzliche "Problem" ist jedoch die Tatsache, dass das mathematische Verfahren wenige bis keine Hinweise auf phänomenologische Aspekte liefert. Eine Dimensionsanalyse erscheint aus erkenntnistheoretischer Sicht erst dann sinnvoll, wenn diese begleitend zu einem konsistenten Denkmodell angewandt wird.

Beispiel: Masse-Energie-Äquivalenz

Mit den Elementarkörper-Gleichungen r(t) und m(t) sowie deren zeitlichen Ableitungen lässt sich dimensionsanalytisch u.a. die Masse-Energie-Äquivalenz E = m₀·c² herleiten.

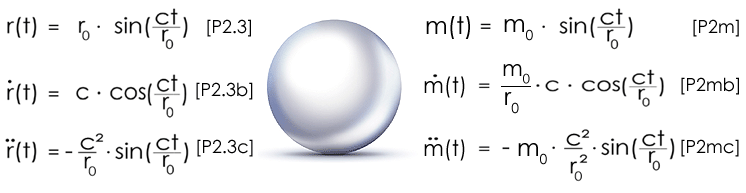
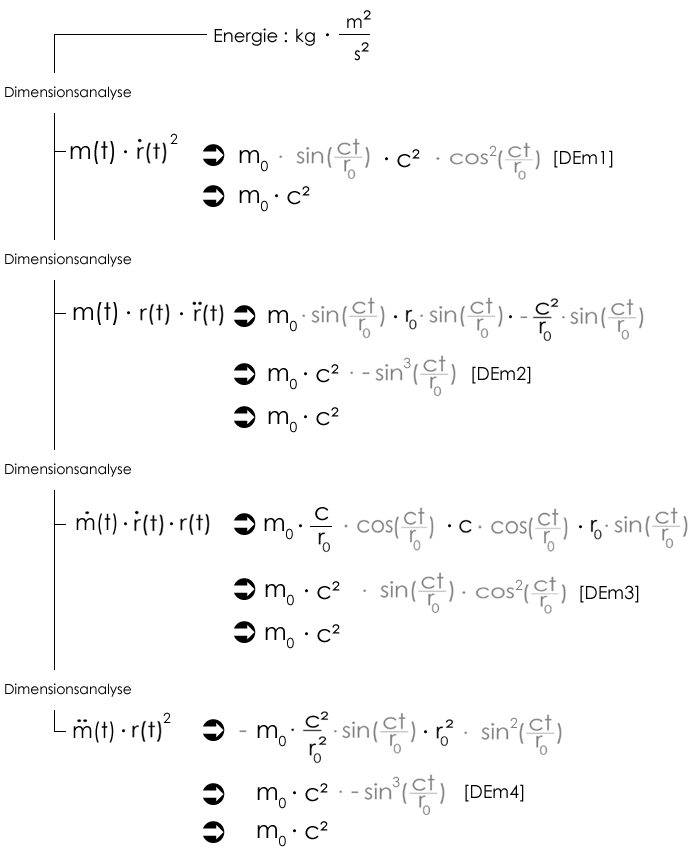
Hier ist ergebnisorientiert (un)mathematisch zu berücksichtigen, dass physikalisch motiviert ausschließlich Beträge und der Maximalwert : 1 der Sinus- und Kosinus-Funktion gewählt werden. Zum Vergleich betrachten wir die phänomenologisch begründete Herleitung der Masse-Energie-Äquivalenz E = m₀·c².

Elementarkörper basierende Herleitung der Energie-Masse-Beziehung E = m0c² Mittels der Gleichungen r(t) = r0sin(ct/r0) [P2.3] und m(t) = m0sin(ct/r0) [P2m] und deren zeitlichen Ableitungen ergibt sich E(t). Da E(t) konstant ist folgt : E(t) ► E = m0c², obwohl zu jedem Zeitpunkt das Verhältnis von Radius abhängiger Energie, respektive Masse abhängiger Energie und Bewegungs-Energie unterschiedlich ist. Da alle auftretenden Grössen dynamisch sind, können wir hier von einem "durch und durch zeitabhängigen" Prozeß "sprechen", welcher nicht im Widerspruch mit der Erhaltung der Gesamt-Energie ist. Es gilt zu beachten, daß trotz des negativen Vorzeichens der zweiten Ableitung von r(t) ► d²r/dt² = (-) (c²/r0²) · r(t) nur die Energie-Beträge IEI der Einzel-Komponenten aus phänomenologischer Sicht relevant sind, da die Änderung der Geschwindigkeit : dv/dt = d²r/dt² stets einen additiven Beitrag zur Gesamt-Energie liefert. Es gibt keine Rückstellkräfte, da es sich um eine Zustandsänderung handelt. Die Änderung der Geschwindigkeit ist  für t≠0 größer Null und endet mit Erreichen von r(t) = r0 und m(t) = m0. Eine rein mathematische Betrachtung, die "formalistisch" einem zeitabhängigen Potential entspricht, ist "sinnfrei".

Zur Erinnerung

Elementarkörper-Entstehung und innere Dynamik

Zum Zeitpunkt t = 0 entfaltet sich eine diskrete Energie-Menge (+E₀) in Gestalt reiner Bewegungs-Energie und bildet einen masse-gekoppelten "Raum" in "Form" einer Kugeloberfläche gemäß der Gleichungen r(t) und m(t) bei stetiger Reduzierung der Expansionsgeschwindigkeit dr/dt. Erkenntnistheoretisch - und wenn man so will philosophisch - "steht" also der Nullpunkt, die "Null", nicht für "Nichts", sondern repräsentiert den maximalen Bewegungszustand. Dieser Zustand entspricht der (zeitlosen) Lichtgeschwindigkeit. Realphysikalisch ist das der masselose Zustand, sprich ein Photon. Das grundsätzliche Mißverständnis ("außerhalb" der Elementarkörpertheorie) besteht darin, daß die Eigenschaften eines wechselwirkenden Photons auf den »Ruhezustand« des Photons projiziert werden. Der »Ruhezustand« des Photons ist jedoch gemäß Gleichung [P2.3] und deren zeitlicher Ableitung [P2.3b], sowie [P2m] der raum- und masselose, „lichtschnelle“ (Energie-)Zustand maximaler Bewegung. Das bedeutet: Das sich gerichtet eine Information ausbreitet, die sich erst bei Absorption des Photons gemäß Gleichungen [P2.3], [P2m] und deren Ableitungen „entfaltet“ und dann die zeitabhängigen messtypischen Phänomene der Interferenz und des (massebehafteten) Stoßes zeigt.

Die Masse-Bildung ist an die zeitabhängige Radius-Vergrößerung r =r(v(t)) gekoppelt. In einfachen Worten: Aus der anfänglichen, reinen Bewegungs-Energie entstehen stetig zeitabhängige Kugeloberflächen, die als solche einen Raum aufspannen, dessen Größe ein Maß für die äquivalente Masse ist. Nach einer Viertelperiode (½π) ist der Elementarkörper voll ausgebildet (r(t) = r₀ , m(t) = m₀), daß bedeutet das die Expansionsgeschwindigkeit v(t) gleich Null ist.

Statischer Zustand des Elementarkörpers und (Teil-)Annihilation

Phänomenologisch ist die Umwandlung von Bewegungsinformation in Rauminformation abgeschlossen. Ohne äußere Wechselwirkung bleibt der Elementarkörper nun in diesem Zustand. Wird der Elementarkörper von außen "angeregt", kommt es zu verschiedenen Wechselwirkungs-Szenarien, die je nach Energie der Wechselwirkungspartner zur Teil-Annihilation oder (Voll-)Annihilation führen. Materiebildende Teil-Annihilationen kommen in der einfachsten Form durch die Proton-Elektron-Wechselwirkung zustande (Stichworte: Rydberg-Energie, Wasserstoffspektrum). Masse gekoppelter Raum annihiliert gemäß r(t) und m(t). "Strahlung" wird aufgenommen oder abgegeben.

Bei der vollständigen Annihilation kontrahiert der Elementarkörper gemäß r(t) und m(t) wieder bis zum Ursprung und liegt sodann in Form reiner Bewegungs-Energie (Strahlung) vor. In dem Zusammenhang ist die Invarianz der [Vakuum-]Lichtgeschwindigkeit auf die beschriebene Zustandsänderung zurückzuführen und nicht auf Mathematik in Form von Bezugssystemen und deren Verknüpfungen.

Beispiel 2: Herleitung und Bedeutung der Gravitationskonstanten

Dimensionsanalytisch lässt sich im Hinblick auf die bekannte Gravitationskonstante γ_G allgemein für Elementarkörper eine charakteristische Größe γ₀ ermitteln, die sich durch das Verhältnis von r₀ zu m₀ definiert. Da für Elementarkörper die Masse-Radius-Konstanten-Gleichung [F1] gilt, existiert eine Beziehung zur kleinsten (skalaren) Wirkung, dem Planckschen Wirkungsquantum h.

Die Gravitationskonstante γ_G  repräsentiert phänomenologisch das Verhältnis von Radius zu Masse des längenkleinsten massereichsten Einzelkörpers (Elementarquant G). Weitere Ausführungen siehe exemplarisch das Kapitel Planckgrössen.