|
Dirac
-
Gleichung
Mit
dem Ziel, eine in sich konsistente relativistische Wellenmechanik zu
konstruieren, stellte Dirac nach dem Vorbild der nichtrelativistischen
Schrödinger-Gleichung eine relativistische Wellengleichung auf, die die
Zeitableitung nur in erster Ordnung enthält. Aus Gründen der
Lorentz-Symmetrie mussten auch die Ortsableitungen in erster Ordnung in
die Gleichung eingehen. Es zeigte sich, daß dies nur mit einem vierkomponentigen
Dirac-Spinorfeld mit der Hilfe von vier Dirac-Matrizen möglich
war.
Die
Dirac-Gleichung beschreibt mit ihren 4 Komponenten Teilchen
entgegengesetzter Ladung (aber gleicher Masse!) in einer gemeinsamen
Gleichung. Die Vertauschung der oberen und unteren Komponenten bedeutet
physikalisch den Übergang zum ‘Gegenteil’: ¨ umgekehrte Ladung,
umgekehrter Impuls, negative Energie, alles in allem einfach das
‘Fehlen’ eines Teilchens, fälschlicherweise* Antiteilchen genannt.
*Der
offensichtliche Selbstbetrug der herrschenden Physik besteht darin,
daß eine Umkehrung der Ladung - beispielsweise aus einem Elektron - kein Antiteilchen gemäß
Einstein-, Dirac- oder Klein-Gordon-Gleichung mit negativer Energie
macht. Die „Antiteilchen“ der herrschenden Physik, wie Positronen
und Anti-Protonen sind somit keine Antiteilchen**. Schon dieses einfache
Beispiel zeigt sowohl die sprachliche als auch inhaltliche „Definitions-Unbestimmtheit“,
sprich „Verwirrung“, sprich Sinnleere innerhalb der herrschenden
Physik auf.
**Dem so genannten »Dirac-See« folgte die Feynman-Stückelberg-Interpretation
für "unerklärliche" negative Energiewerte der
Dirac-Gleichung. Im Bild der
Quantenmechanik "löste" man dieses Problem vermeintlich mit
Hilfe der Heisenbergschen Unschärferelation, indem man die
entsprechenden Lösungen willkürlich als Entitäten mit positiver
Energie interpretiert, die sich rückwärts in der Zeit bewegen. Das
negative Vorzeichen der Energie wird auf die Zeit übertragen (Feynman-Stückelberg-Interpretation).
Dirac verstand unter dem Dirac-See das Vakuum als einen unendlichen
"See" von Teilchen mit negativer Energie, ohne weitere freie
Plätze für negative Energien (?!?). Man muß(te) wahrscheinlich Dirac,
Feynman oder Stückelberg heißen, um sich solch naiven
"Zauber" leisten zu können. Der Wille fehlende Anschauung
sprich fehlende konsistente (Begriffs-)Phänomenologie
durch formale Hilfskonstruktionen bzw. wilde Fantasien zu ersetzen ist
überdeutlich. Mathematisch ist das kein Problem, erkenntnistheoretisch
schon.
Dirac-Gleichung
und g-Faktor - Anfang und Ende [neo]barocker
Theoriefantasien
Die
Herleitung des so genannten g-Faktors (gyromagnetischer Faktor, Landé-Faktor)
= 2 mittels der Dirac-Gleichung
setzt voraus, daß die Geschwindigkeit des Teilchens klein ist. Bei
genauer Sicht wird nicht nur die kinetische Energie sondern auch die
elektrostatische Energie als klein gegenüber der Ruheenergie
angenommen. Es handelt sich also bei der Bestimmung des Wertes g = 2
schon im Ansatz um eine Näherung. Umso verblüffender ist nun aus
logischer Sicht die „Überraschung“ der Protagonisten der
Systemphysik, daß der experimentelle Wert für den g-Faktor des
Elektrons nicht genau 2 entspricht. Ernsthaft: Wie kann ein
approximierter Wert als exakter Erwartungswert gelten?
Mit
anderen Worten: Es ist alles andere als verwunderlich, daß der
experimentelle Wert für das magnetische Moment des Elektrons (g = 2,002 319 304 361 82(52))
nicht dem theoretisch berechneten Erwartungswert entspricht. [Zum Myon
kommen wir später im „eigentlichen Artikel“] Losgelöst von der
exakten quantitativen Abweichung, lassen die gewählten Näherungsbedingungen
der Dirac-Gleichung diese als qualitative „Ursache“ erkennen. Bei
der Berechnung des g-Faktors fehlt der Dirac-Gleichung - salopp
formuliert – offensichtlich ein Teil der Wechselwirkungsphysik. Um
diese Physik (energetisch) verstehen zu können, müsste man das
elektrische sowie das magnetische Feld „phänomenologisieren“. Denn
Felder (elektrisch, magnetisch, gravitativ) sind sekundäre Begriffe
respektive sekundäre Größen. Der „eingeschlagene“ Weg über die
QED liefert zwar sehr gute Korrekturen aber diese liefert keine
(konsistente) Phänomenologie.
Halten
wir fest: Das der g-Faktor für das Elektron nicht wie theoretisch
approximiert 2 sondern (-) 2,00231930436182 beträgt, führen
Quantenfeldtheoretiker auf notwendige Korrekturen zurück, die hauptsächlich
mittels Quantenelektrodynamik - und zu kleineren Teilen
quantenchromodynamisch - begründet sind. Das Minuszeichen (-) gibt an,
das die QM-theoriebeladene Messung des magnetischen Momentes eine
Erwartungsrichtung vorgibt und der Messwert nicht der
"Erwartungsrichtung" entspricht.
„Vergessen“
wir nun QED, QCD, allgemein Standardmodellfantasien. Qualitativ ist aus
logischer Sicht sofort klar, daß magnetische und elektrische Felder bei
der Bestimmung der magnetischen Momente (siehe exemplarisch die
Doppel-Penning-Falle) mit dem massebehafteten Ladungsträger
wechselwirken. Mit der Annahme, daß nun die angelegten Felder
versuchsinhärent zum magnetischen Moment beitragen, ergibt sich eine
plausible Erklärung und insbesondere für Quantenfeldtheoretiker eine
unerwartete, erstaunlich gute Alternative zur QED. Mit dem Ergebnis, daß
die magnetischen Momente des Elektrons, Protons (und auch des Neutrons)
sich masse-radius-gekoppelt berechnen lassen. Im Rahmen eines
realobjektfreundlichen Denkmodells erscheint die Quarks basierende, u.a.
25 freie Parameter lastige QCD als komplex-epizyklisch*.
[Begriffsbestimmung
komplex-epizyklisch* Sowohl die Epizykeltheorie aus heutiger Sicht als
auch das Standardmodell der Teilchenphysik (SM) als
quantenfeldtheoretische Anwendung und Weiterentwicklung der
Quantenmechanik basieren auf Fourier-Reihen respektive
Fourier-Transformierte. Die Epizykeltheorie arbeitete mit 3 freien
Parametern, war mathematisch „richtig“, phänomenologisch falsch und
die Objekte der Beschreibung waren (sind) sichtbar (Auge, Fernrohr). Das
SM arbeitet mit 25 freien Parametern, variablen Kopplungskonstanten,
virtuellen Teilchen, theorieinduzierten, nicht realen Objekten und
keines der Objekte ist sichtbar.]
Fazit:
"Verkörpert" man das magnetische Feld in einer
"energetischen Analogie" so resultieren das messtechnisch
erfasste magnetische Moment des Protons und des Elektrons aus der
jeweiligen energetischen Überlagerung mit dem Magnetfeld. Das
Magnetfeld selbst als „Energiegeber“ ist in Wechselwirkung mit
Elektron und Proton und liefert einen
"teilchenspezifischen" Beitrag in der Größenordnung von ~
1e-26 Joule/Tesla zum gemessenen magnetischen Moment. Das bedeutet: Der
ganze mathematische QFT-Zauber um vermeintlich anomale (intrinsische)
magnetische Momente und deren Korrekturen sind theorieinduziert, oder
schlichter formuliert - im wahrsten Sinne des Wortes - gegenstandslos.
Des Weiteren folgt daraus: Das experimentell bestimmte magnetische
Moment des Protons ist (nunmehr) ohne Substruktur plausibel.
In
einfachen Worten: Die Annahme, daß Beiträge zum magnetischen Moment
der materiebildenden primären Ladungsträger in einem äußeren
Magnetfeld messungsinhärent aus dem Feld kommen und nicht intrinsisch
sind, wird zahlenanalytisch, naturphilosophisch als auch formal
untersucht und bestätigt. In dem Zusammenhang ist das Neutron
masse-radius-gekoppelt Elektron-Proton basierend. Siehe: Anatomie
der anomalen magnetischen Momente und das
Neutron.
Das
Elektron ist quantenfeldtheoretisch ohne Ausdehnung, somit ohne Trägheitsmoment
daraus folgend realphysikalisch „eigendrehlos“. Es existiert eine
rein energetische Analogie, die sich durch Energieniveau-Aufspaltungen
manifestiert. Mit einer Eigendreh-Dynamik des Elektrons hat das nichts
zu tun. Des Weiteren ist die „Extrapolation“ vom Bohrschen Magneton
hin zum intrinsischen magnetischen Moment des Elektrons, wie im Kapitel
»Spin« gezeigt wird, im Rahmen
formaler „Denkmodelle“ phänomenologisch vollkommen unbegründet.
Fazit:
Spin-Bahn-Wechselwirkung gemäß Dirac und "semiklassische"
relativistische Korrektur ohne Spin sind im Ergebnis gleich! Der
quantenmechanische Spin "entsteht rein mathematisch"
mittels so genannter γ-Matrizen "innerhalb" eines
Gleichungssystems. Wer Freude an mathematischen Ausführungen hat, kann
dies in zahlreichen Abhandlungen selbst recherchieren.
Übrigens:
Der »spin« und das »magnetische Moment« sind – entgegen häufig geäußerter
Behauptung – nicht nur Ergebnisse der Dirac-Gleichung. Der erste
Hinweis darauf, dass man die Pauli-Gleichung samt magnetischem Moment
des Elektrons auch ganz im Rahmen einer nichtrelativistischen Theorie
herleiten kann, stammt von Galindo.
A. Galindo, Sanchez del Rio, Am.J.Phys. 29, 582 (1961) Die Pauli-Gleichung
geht auf den österreichischen Physiker Wolfgang Pauli zurück. Sie
beschreibt die zeitliche Entwicklung eines geladenen Spin-1/2-Teilchens,
das sich „langsam“ im elektromagnetischen Feld bewegt, so dass die
Feldenergie und die kinetische Energie klein gegen die Ruheenergie sind,
also ein eindeutig nichtrelativistisches Szenario.
Wie in der klassischen Physik entspricht der QM-Ansatz zur Lösung der
Schrödinger-, Pauli- oder Dirac-Gleichung der Idee eines bewegten
Teilchens (Elektrons). Genau genommen wurde das klassische
„himmelsmechanischanaloge“ (Bohrsche) Denkmodell des
Wasserstoffatoms in die Quantenmechanik hineinkopiert. Es resultieren
zwar im Zuge der theoretischen Weiterentwicklungen den verwendeten
Formalismen zusätzliche Korrekturterme zur Energie(aufspaltung), doch
die Kernidee eines bewegten Elektrons um einen "Zentralkörper"
bleibt primär die Ausgangsbasis (siehe Hamiltonoperator) der
Betrachtung.

Magnetische Moment
des Myons
Das
Myon wird vom Standardmodell als strukturloses
Lepton mit einer mittleren Lebensdauer von ~
2,19698e-6s betrachtet. Das
"anomale" magnetische Moment des Myons
wird im Standardmodell wie folgt
"berechnet".
Massenabhängige
QED-Beiträge: In
dieser Klasse sind Schleifenbeiträge mit virtuellen
Photonen und anderen Leptonen zusammenfasst. Sie
treten erst ab dem Zweischleifenniveau auf. Beim
Myon kann man zwischen Schleifeneinsetzungen mit dem
leichteren Elektron und dem schwereren Tauon
unterscheiden. Erstere führen auf große
Logarithmen der Form log(mµ/me), während letztere
vergleichsweise geringe Korrekturen aufbringen, die
bei der Präzision des Brookhaven-Experiments jedoch
relevant sind. Die Ungenauigkeiten dieser Klasse von
Beiträgen stammen aus der Ungenauigkeit der
Massenverhältnisse mµ/me und mµ/mτ.
Insgesamt stellen die QED-Beiträge die größten
Korrekturen dar. Zum heutigen Zeitpunkt sind sie auf
Dreischleifenniveau analytisch und auf
Vierschleifenniveau numerisch bekannt.
Hadronische
Vakuumpolarisation: Da
Quarks keine freien Teilchen sind, sondern
hadronisieren, lassen sich ihre Beiträge nicht
durch eine Schleifenentwicklung ermitteln. Im Falle
der Vakuumpolarisation kann man sich allerdings
behelfen und die relevante
Photon-Selbstenergiefunktion aus Messungen von e +e
− → γ* → hadrons bestimmen.
Hadronische
Photon-Photon-Streuung:
Im Gegensatz zur Vakuumpolarisation kann sich die
hadronische Photon-Photon-Streuung nicht auf
experimentelle Daten berufen. Hier muss man sich
daher auf effektive Niedrigenergiebeschreibungen der
QCD wie die Chirale Störungstheorie stützen, in
denen der Hauptbeitrag zu dieser Klasse von
Diagrammen durch den Austausch von π0
und anderen Mesonen beschrieben wird. Ingesamt sind
die hadronischen Beiträge für den Großteil der
Ungenauigkeit des theoretischen Ergebnisses
verantwortlich.
Elektroschwache
Beiträge: Aufgrund
der hohen Masse der W± -, Z0
- und Higgsbosonen sind diese Beiträge stark
unterdrückt, jedoch beim Brookhaven-Experiment
wegen dessen hoher Präzision erstmals nicht
vernachlässigbar. Generell lässt sich diese Klasse
von Diagrammen in bosonische Beiträge und Beiträge
mit geschlossenen Fermionschleifen unterteilen.
Letztere sind besonders kritisch, da hier Auslöschungen
mit den verwandten Quarkschleifenbeiträgen zur
Erhaltung der Anomaliefreiheit in der SU(3)C x
SU(2)L x
U(1)Y Eichtheorie stattfinden. Die Ungenauigkeit der
elektroschwachen Beiträge ist hauptsächlich durch
die Ungenauigkeit von sin θw und der
Higgsmasse begründet.
Die
Abweichung zwischen Standardmodell-Vorhersage und
dem Ergebnis des Brookhaven-Experimentes entspricht
einer Diskrepanz von 3,2 σ. Andere Auswertungen
haben eine Diskrepanz von 3,4 σ bis 3,6 σ
ergeben.
Theorie
und Experiment zur Bestimmung des magnetischen
Moments des Myons werden in http://www-com.physik.hu-berlin.de/~fjeger/gm2review.pdf
nachvollziehbar beschrieben.
Elementarkörper
basierend ist das Myon schlicht ein instabiler
Elementarkörper. Das Myon wandelt sich gemäß der
inhärenten Masse-Radius-Kopplung in ein Elektron,
masseabhängige Energie des Myons wandelt sich in
radiusabhängige Energie des Elektrons.
Da
sich das Myon offensichtlich nicht spontan in ein
Elektron umwandeln kann, ist die Angabe eines
konkreten magnetischen Moments des Myons eine „Meß-Fiktion“.
Insgesamt ist zu bemerken, daß das magnetische
Moment des Myons nicht direkt gemessen wird.
update
19.10.2021
Ein „Myon“- Gedankenexperiment
Da
das Myon Bestandteil der Zerfallskaskade Pion* ►
Myon ► Elektron ist, nehmen ich in diesem
Gedankenexperiment an, das der inhärente
Magnetfeld-Beitrag zum magnetischen Moment des Myons
der des Elektrons (ungefähr) entspricht. Für eine
konkrete Berechnung setzte ich diesen gleich dem
Anteil des Elektrons.
Daraus resultiert:
4,49044830e-26 J/T - 1,07546279e-26 J/T =
3,41498551e-26 J/T = [μBμ(th)]
Rechnet man das zurück auf
die semiklassisch definierte Masse in Abhängigkeit
des magnetischen Moments m([μBμ(th)]) so ergibt sich
ein Wert von 2,47381765e-28 kg. Das entspricht ~
0,994274 · mπ der Masse geladener Pionen.
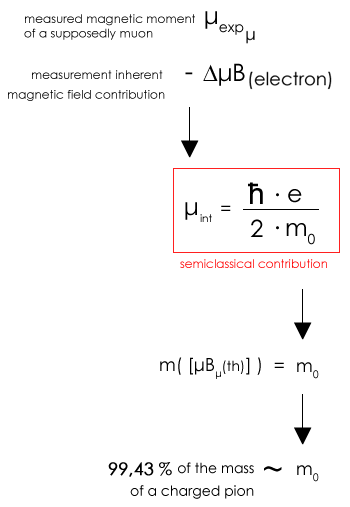
mπ = 2,4880644e-28 kg = 139,570180 MeV/c²
Das führt zu der These, dass im vermeintlichen
Myonen-g-2-Experiment nicht das magnetische Moment
des Myons sondern das des (geladenen) Pions
gemessen wird**.
**Im Rahmen des SM besitzen Pionen keinen Spin und
kein magnetisches Moment. Was hier nicht weiter
stört, da das SM in dieser Betrachtung eh außen vor
ist.
Wie “unnatürlich“ Pionen
im SM postuliert und konstruiert werden ist u.a. dem
bevorzugten mathematischen Erfassungsmechanismus
geschuldet. Mittlerweile sind alle experimentellen
Anordnungen und Meßdateninterpretationen den
theoretischen Vorgaben angepasst.
Das geladene Pionen zu ~
99,99% sich in Leptonen sprich Myon und Myon
Neutrino umwandeln sollen und das neutrale Pion,
welches eine um ~ 3% geringere Masse als die
elektrisch geladene Version besitzt, sich zu 98,82 %
in zwei Photonen umwandelt, sollte bereits
phänomenologisch zu denken geben. Die Betrachtung
respektive Konstruktion eines konsistenten
phänomenologischen Ansatzes gestaltet sich insgesamt
als schwierig, da die Gesamtheit der postulierten
Pionen-Umwandlungsprozesse eine ganze Reihe von
neuen Wirkmechanismen erfordert, die auch
mathematisch wechselwirkend und verschachtelt werden
müssen.
Wie sieht die
weitere Implementierung im Hinblick auf weitere
postulierte Theorieobjekte aus? Gemäß SM „bedeutet“
Neutrinoforschung beispielsweise:…Man
misst die Ströme der
Kaonen und
Pionen und bestimmt indirekt den Fluss der
Neutrinos…
Wie kurz
angedeutet sind aber schon Pionen (π0, π -, π+) höchst
konstruierte Gebilde und erst recht Kaonen (K+,
K-, K0, K0)
des Standardmodells. Bedeutet: Die Anzahl der
Existenzpostulate, wie Masse, Ladung, Spin,
flavor(s), Lebensdauern und Quarkzusammensetzung ist
bereits „beachtlich“. Die möglichen Umwandlungen
ergeben „ vielfältige“ Wechselwirkungs--Szenarien.
Des Weiteren: Das neutrale Kaon ist nicht sein
eigenes „Antiteilchen“, dies führt (allgemeiner) zu
der Konstruktion der
Teilchen-Antiteilchen-Oszillation und das
neutrale Kaon soll in zwei Formen, einer langlebigen
und einer kurzlebigen Form existieren.
Daraus nun auf Eigenschaften „flavor-oszillierender“
Neutrinos zu schließen, potenziert die
Beliebigkeit nochmals. Übrigens:
Es gibt keinen einzigen direkten Neutrinonachweis.
Es handelt sich stets um stark theoriebeladene
Versuchsergebnisinterpretationen.
Um das alles
(reproduzierbar) zu verstehen, braucht man den absoluten Glauben an axiomatische Schöpfungen.
Als Belohnung
winkt dann jedoch der Freibrief, daß jedwedes
Versuchsergebnis „erklärbar“ wird (…das wir bis
dahin - in Verbindung mit der »experimentellen
Seite« - grob geschätzt einige Dutzend weitere
ergebnisorientierte Annahmen machen müssen, …
kümmert SM-Gläubige nicht).
Da sich
das Pion offensichtlich nicht spontan in ein Myon
umwandeln kann und ein Myon sich nicht spontan in
ein Elektron umwandelt, ist die Angabe eines
konkreten magnetischen Moments des Myons eine „Meß-Fiktion“.
Insgesamt ist zu bemerken, dass das magnetische
Moment des Myons nicht direkt gemessen
wird. Konsequent weiter gedacht, stellt sich u.a.
die Frage nach der effektiven Masse des Myons in den
g-2-Experimenten.
Zum
Mitdenken
In
Verbindung mit der „ g=2 - erzeugenden“
Dirac-Gleichung gibt es ein fundamentales „Näherungs-Problem“
erster Instanz für das Myon. In der Dirac-Gleichung
wird zur Berechnung von g = 2 vorausgesetzt, daß das
zu beobachtende „Dirac-Teilchen“ sich langsam
bewegt, daß ist im Falle der experimentellen
Bestimmung des magnetischen Moments des Myons,
welches sich im Speicherring mit einer
relativistischen Geschwindigkeit (Ekin ~ 30 · E0 !) bewegt
definitiv nicht der Fall. Aus diesem Grunde kann die
Dirac-Gleichung formal logisch für das Myon gar kein
Ergebnis für g liefern. Ohne g = 2 existiert aber
kein „normales“ magnetisches Moment des Myons und
folgerichtig ist das „anomale“ magnetische Moment
des Myons ohne („normale“) Referenz
gegenstandslos. Will man also mittels
Dirac-Gleichung eine Aussage über das (normale)
magnetische Moment des Myons machen, dann kommen nur
Experimente in Frage, in denen sich das Myon
„langsam“ bewegt.
*Dass
Pionen anders als das Elektron und das Myon im Rahmen des SM postuliert
aus (up- und – down) Quark- und Anti-Quark bestehen
sollen ist wenig hilfreich und genauer gesagt
phänomenologisch mehr als fragwürdig.
Pionen sind Fermion-Antifermion-Paare. Ergänzend sei
bemerkt: Aus der Dirac-Gleichung folgt, dass das
Produkt der (Eigen-)Paritäten von Fermion und
Antifermion gleich –1 ist. Es gibt daher zwei
Möglichkeiten die Paritäten von Quarks zu
definieren: P(Quark) = –1 und P(Antiquark) = 1, oder
P(Quark) = 1 und P(Antiquark) = –1. Da Pionen (wie
alle Mesonen) aus Quark und Antiquark bestehen, gibt
das in beiden Fällen einen Faktor –1 für das Produkt
der Eigenparitäten (für die Gesamtparität spielt der
relative Bahndrehimpuls auch noch eine Rolle). Da
Nukleonen postuliert aus 3 Quarks bestehen, ist das
Produkt der Eigenparitäten +1 bzw. –1, je nach
Definition.
Wie erwähnt, im Rahmen des SM besitzen Pionen keinen
Spin und kein magnetisches Moment. Die Beliebigkeit
der SM-Aussagen bezüglich der Pionen findet eine
weitere Steigerung in Form des ungeladenen Pions,
was zum postulierten
Quarkonium führt.
Der Vollständigkeit halber erwähnt: Das Pionen im
SM-Denken doch irgendwie (geringfügig) zu
magnetischen Momenten beitragen sollen,
verdeutlichen die folgend exemplarisch aufgeführten
Ausarbeitungen...
Pion contributions to baryon magnetic moments 1984
by Jerrold Franklin
Charged Pion Contribution to the Anomalous Magnetic
Moment of the Muon 2013 by Kevin Engel
Pion-Loop Contribution to the Anomalous Magnetic
Moment of the Muon 2013 by B.Sc. Jan Hass
Im Rahmen der Elementarkörpertheorie lassen sich
Pionen als geladene Pionen aus der Proton-Elektron-q0-q0-Wechselwirkung
und ungeladen aus der Elektron-Positron--q0-q0-Wechselwirkung
bilden.
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Bis zum 18.10.2021 galt
im Rahmen einer Plausibilitätsbetrachtung die
Aussage...
[„Interessanterweise“
ist bei der indirekten experimentellen Bestimmung
des magnetischen Moments des relativistischen Myons
im Ergebnis das magnetische Moment – anders als bei
Proton, Elektron und Neutron – von dem additiven
Magnetfeldbeitrag befreit. Die relativistische
Bewegungsenergie kompensiert (nahezu) den
Energiebeitrag des Magnetfeldes zum magnetischen
Moment. Dieser Sachverhalt erschließt sich den
Standardmodelldenkern nicht, da das Magnetfeld nicht
als Energieträger „wahrgenommen“ wird.]
::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::::
Konsequent weiter gedacht, stellt sich die Frage
nach der effektiven Masse des Myons in den
g-2-Experimenten (exemplarisch am Brookhaven National
Laboratory 1997-2001). Aus Sicht der Elementarkörpertheorie
bestätigt somit auch die Messung des magnetischen
Moments des Myons die bisherige Sicht der Dinge.
Zum
Mitdenken:
In Verbindung
mit der „ g=2 - erzeugenden“ Dirac-Gleichung
gibt es, wie bereits ausgeführt, ein fundamentales
„Näherungs-Problem“ erster Instanz für das
Myon. In der Dirac-Gleichung wird zur Berechnung von
g = 2 vorausgesetzt, daß das zu beobachtende
„Dirac-Teilchen“ sich langsam bewegt, daß ist
im Falle der experimentellen Bestimmung des
magnetischen Moments des Myons, welches sich im
Speicherring mit einer relativistischen
Geschwindigkeit (Ekin ~ 30 ·
E0 !) bewegt
definitiv nicht der Fall. Aus diesem Grunde kann die
Dirac-Gleichung formal logisch für das Myon gar
kein Ergebnis für g liefern. Ohne g = 2 existiert
aber kein „normales“ magnetisches Moment des
Myons und folgerichtig ist das „anomale“
magnetische Moment des Myons ohne („normale“)
Referenz gegenstandslos.
Will man also mittels Dirac-Gleichung eine Aussage
über das (normale) magnetische Moment des Myons
machen, dann kommen nur Experimente in Frage, in
denen sich das Myon „langsam“ bewegt.
|
|
|
Vorgeschichte
Quantenmechanisches
Spin-Postulat und Epizykeltheorie
Die
omnipräsenten pathologischen Beschreibungs-Prozeduren
herrschender Physik(-Didaktik) mittels Begrifflichkeiten wie
Spin oder Spin-Bahn-Wechselwirkung suggestiv an
realphysikalische Objekte gedanklich "anzukoppeln",
die Masse besitzen, Raum einnehmen und rotieren, ist seit Einführung
der Quantenmechanik schizophren. Bedenke: Dem Elektron wird
per Postulat ein Radius "abgesprochen". Protonen
sind asymmetrisch ladungsfragmentiert, asymmetrisch
substrukturiert und deren Quarks liefern u.a. nur ein Prozent
der Protonenmasse und - wie bereits bemerkt - keine
intrinsischen Spinbeiträge. Diskrete Bahnen wurden durch
Wahrscheinlichkeits-Wellenfunktionen ersetzt, die zu
"wahrscheinlichen", "verschmierten" Orten
und Impulsen führen.
Schizophren
auch deshalb, weil im gleichem Atemzuge der analog-mechanisch
motivierten Suggestion dann wieder explizit geäußert wird,
das es ja nicht so ist, wie in zahlreichen Illustrationen und
semantischen Absonderungen propagiert wird.
Literatur-Beispiel:
Kapitel
10.2 Diracsche Elektronentheorie 1928 Seite 10006 Zitat
…“Denn der neue Drehimpuls hat mit dem, was man sich unter
diesem Namen als mechanische Größe vorstellen kann, nichts
mehr gemein. Er entsteht aus keiner Bewegung, sondern aus dem
Zusammenwirken eines räumlichen Vektors mit den
Dirac-Matrizen in dem Raum ihrer vier abstrakten
Dimensionen.“…
Quelle:
http://www.iup.uni-bremen.de/~bleck/lecture_notes/KT-15Kap.pdf/Kap-10-Elektron_Positron_Leptonen.pdf
Aus
dieser Betrachtung folgt, daß alle theoretischen Ausführungen
und Berechnungen zu Spin-Wechselwirkungen
("Spin-Bahn-Kopplung" ► Feinstruktur,
Kernspin-"HüllenDrehimpuls" ►
Hyperfeinstruktur) keine Anschaulichkeit besitzen. Es
sind lediglich - mehr oder weniger - komplexe
Rechenvorschriften ohne Realobjekt-Anbindung. An dieser Stelle
offenbart sich exemplarisch das Dilemma quantenmechanischer
Betrachtungen. Aus einer Schar von quantenmechanischen
Rechenvorschriften lassen sich Spektrallinien-Aufspaltungen
berechnen. In diesem Zusammenhang ist aber jedwede Verbindung
zu realphysikalischen Objekten gekappt. Die Frage, warum
mathematische Verfahren Lösungen liefern, die man
experimentellen Werten zuordnen kann, ist auf Grund der
fehlenden Phänomenologie nicht zu beantworten. Darüber
hinaus stellt sich grundsätzlich die Frage, inwieweit Meßbares
intrinsisch ist? Der
generelle Denkfehler liegt in der methodischen Vernachlässigung
der Struktur - der von „aussen“ eingebrachten -
Wechselwirkungs-Energie. Energieaufspaltungen sind meist nicht
selbstinduziert. Durch das "Anlegen" von
homogenen oder inhomogenen elektrischen Feldern oder
Magnetfeldern wird von aussen eine "energetische Störung"
eingeführt. Phänomenologisch sind physikalische Felder
unbegründet. Sie stellen aus Sicht eines zu untersuchenden
Objektes (…Elektron, Atom, Molekül) unendliche
Energie-Reservoirs dar, welche mit den zu untersuchenden
"Test-Objekten" wechselwirken. Um
diese mehr oder weniger willkürliche Situation zu beenden, wäre
es zwingend die „Feld-Phänomenologie“ spektroskopischer
Messungen zu bestimmen. Das ist im Rahmen der mathematisch
begründeten QM weiterführend QED und QCD im Rahmen des
Standardmodells der Teilchenphysik sowie deren
(Symmetrie-)Erweiterung (Supersymmetrie) nicht möglich,
da die Objekte der Theorien allesamt keinen realphysikalischen
Anspruch besitzen.
|
Betrachtungen und Details zum Verständnis
Phänomenologisch basierende
Berechnung anomaler magnetischer Momente
Spin und magnetische
Momente

|

